前言
SimRank是一种基于图的推荐算法。思想与协同过滤算法相似:
- 如果两个用户相似,则与这两个用户相关联的物品也类似;
- 如果两个物品类似,则与这两个物品相关联的用户也类似。
SimRank应用于可以构建二部图的推荐场景。所谓二部图就是图中的节点可以分成两个子集,而图中任意一条边的两个端点分别来源于这两个子集。如图1,将用户和物品的购买行为构建成一个二部图。从图中也可以看出,二部图的子集内部没有边连接。左边的用户节点形成一个点集,右边的物品节点行形成另一个点集,用户和物品之间的购买行为则构成了二部图的边。
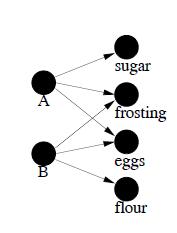
通过SimRank,我们可以得到用户之间的相似度,以及物品之间的相似度,继而进行一些实际的推荐应用。
Bipartite SimRank(朴素SimRank)
Bipartite SimRank就是原始SimRank基于二部图的实现模型,即朴素SimRank。(原始SimRank是利用有向图解决结构化文本相似度的理论模型)[4]
设二部图为$G(V,E)$,其中$V$是节点集合,$E$是边集合。A和B为任意两个用户,对于用户集合中两个用户的相似度公式为:
$$
s(A,B)=\frac{C_1}{|O(A)||O(B)|}\sum_{i=1}^{|O(A)|}\sum_{j=1}^{|O(B)|}s(O_i(A), O_j(B))
\tag{1}
$$
设c和d为任意两个物品,对于物品集合中两个物品的相似度公式为:
$$
s(c,d)=\frac{C_2}{|I(c)||I(d)|}\sum_{i=1}^{|I(c)|}\sum_{j=1}^{|I(d)|}s(I_i(c), I_j(d))
\tag{2}
$$
其中$I(a)$为节点a的入邻节点,$O(a)$为出邻节点,$C_1$和$C_2$为阻尼系数。
综上可以看出,式(1)和式(2)非常相似。所以我们可以将有向二部图看成无向图,即删去边的方向。所有节点通过边相连的节点都视为其的入邻节点。另外一般赋值$C_1=C_2=C$。于是朴素SimRank的公式如下:
$$
s_0(a,b)=\begin{cases}
0 & (a\neq{b})\
1 & (a=b)
\end{cases}
$$
$$
s_{k+1}(a,b)=\frac{C}{|I(a)||I(b)|}\sum_{i=1}^{|I(a)|}\sum_{j=1}^{|I(b)|}s_k(I_i(a), I_j(b))
$$
其中$s_k(x,y)$表示第k轮迭代中两个节点的相似度。
矩阵化
为方便计算和分布式实现,需要将上式转化为矩阵计算。注意到上式可以转化为:
$$
\begin{aligned}
s_{k+1}(a,b)=\frac{C}{|I(a)||I(b)|}\sum_{i=1}^{|I(a)|}\sum_{j=1}^{|I(b)|}s(I_i(a),I_j(b)) \
=C\sum_{i=1}^{|V|}\sum_{j=1}^{|V|}p(v_i,a)s_k(v_i,v_j)p(v_j,b)
\end{aligned}
\tag{3}
$$
其中$V$是二部图节点集合,$k$是当前迭代的轮数,$v_i$为$V$中第$i$个节点。$p(v_i,a)$表示节点$v_i$到节点$a$的转移概率,其公式为:
$$
p(x,y)=\frac{e(x,y)}{|E(y)|}=\frac{e(x,y)}{\sum_{i=1}^{|V|}e(x,v_i)}
\tag{4}
$$
$$
e(x,y)=\begin{cases}
1 & x和y相邻 \
0 & x和y不相邻
\end{cases}
$$
于是,节点间的相似度矩阵S的计算公式为:
$$
S_k=\begin{cases}
CP^TS_{k-1}P+I_n-Diag(diag(CP^TS_kP)) & k > 0 \
I_n & k=0
\end{cases}
$$
其中,矩阵S的元素$s_{i,j}=s(i,j)$,节点间的相似度。$P$是二部图的邻接矩阵按行归一化后的转移概率矩阵,即$P$每一行元素和为1。$I_n$是$n*n$的单位矩阵。$diag(M)$函数是取矩阵M的对角向量,$Diag(V)$是将向量V转为一个对角矩阵。因为相似度矩阵S中,节点自己与自己的相似度为1,所以需要加入修正项。
SimRank++
朴素SimRank会有以下存在问题。
- 节点的(另一个子集)连接节点集合越大,则与这个节点相似的节点相似度会越小。
- 没有考虑边的差异,即没有考虑边的权重。
为了解决这些问题,Antonellis等提出了SimRank++算法[3]。其主要做了以下两点
改进。
- 考虑节点相似度证据。
- 加入边的权重。
节点相似度证据
对于为什么加入节点相似度,请阅读文章[1]第三章的例子,本文不再赘述。简单的来说就是,关系越简单(相连边少)的节点更容易与其他节点相似,关系越复杂(相连边多)的节点更难与其他节点相似,朴素SimRank缺乏考虑节点的共同相邻点集的大小。
对于节点a和b,他们的相似度证据为:
$$
evidence(a,b)=\sum_{i=1}^{|E(a)\cap{E(b)}|}\frac{1}{2^i}
$$
其中$E(a)$表示节点的相邻节点集。可以看到相似度证据是个小于1的值,当a与b的共同相连点集最大,相似度证据越大。
于是带证据的相似度公式为:
$$
s_{evidence}(a, b)=evidence(a,b)\cdot{s(a,b)}
$$
因为SimRank有多轮迭代,而相似度证据只需要计算一次,所以节点相似度证据在SimRank迭代完最后再计算。
加入边的权重
在互联网广告中,用户点击1次商品A和点击1000次商品B的意义是不同的,显然商品B对于用户更相关。同样的,用户A点击1次商品i,而用户B点击100次商品i,用户C点击100次商品j,用户D点击100次商品j,我们可以得出用户C和D更相似,而A和B则不相似。所以边的权重是非常重要的因素,SimRank考虑边的权重是必要的。
朴素SimRank中式(4)表示了节点之间的转移概率,每条边的权重都为1,表示节点间有无边相连。现我们将边的权重设为边的数量,即节点间的连接数(例子中点击的数量),然后归一化。改进后的节点间的带权转移概率为:
$$
p_w(x,y)=e^{-var(y)}\frac{w(x,y)}{\sum_{i=1}^{|V|}w(x,v_i)}
$$
$$
特别p_w(x,x)=1-\sum_{i=1}^{|V|}p_w(x, v_i)
$$
$$
var(y)=\frac{\sum_i^{|E(y)|}(w(E_i(y),y)-\mu_y)^2}{|E(y)|}
$$
其中$w(x,y)$表示节点x和y之间的边数(x对y的点击数)。$var(y)$即y的所有邻边的权重方差,可见方差越大,权重越小。
于是,节点间的相似度矩阵S的计算公式改为:
$$
S_k=\begin{cases}
CW^TS_{k-1}W+I_n-Diag(diag(CW^TS_kW)) & k > 0 \
I_n & k=0
\end{cases}
$$
$W$是二部图的带权转移概率矩阵,元素就是$p_w(i,j)$。
完整SimRank++算法步骤
输入: 阻尼系数$C$,迭代词数$k$,带权转移矩阵$W$,证据矩阵$V$
输出: 节点相似度矩阵$S$
程序:
- $S = I_n$
- for 第i次迭代
$temp=CW^TSW$
$S=temp+I_n-Diag(diag(temp))$
end for - $S=S*V$
python demo
更新中
延伸思考
Q: SimRank与协同过滤等传统推荐算法相比有什么优点和缺点?
References
[1] http://xudongyang.coding.me/simrank-plus-plus/
[2] https://www.cnblogs.com/zhangchaoyang/articles/4575809.html
[3] Simrank++: Query Rewriting through Link Analysis of the Click Graph
[4] SimRank: A Measure of Structural-Context Similarity